Regular Polyhedra

Home

This page presents all the regular polyhedra in rotating animations created using Matlab. Click on the polyhedra images to see the animations.

Skip to the coloured regular compounds!

Icosahedron stellations page

Uniform polyhedra page

Platonic solids

The five regular convex solids were known to Euclid and Plato (as the name suggests).

There is a simple proof that no more than five convex regular solids are possible: at least three faces must meet at each vertex and the sum of their angles must be less than 360 degrees; the only possibilities are therefore 3, 4 or 5 equilateral triangles, 3 squares or 3 regular pentagons. It is less obvious, but all these cases are actually possible.

	The tetrahedron is the simplest regular polyhedron, having only four triangular faces. It occurs in several symmetrical compounds: the Stella Octangula, two forms of five tetrahedra, and ten tetrahedra.
	The cube is a familiar, useful shape. It is reciprocal to the octahedron. It occurs in a compound of five.
	The octahedron has eight triangular faces and is reciprocal to the cube. It also occurs in a compound of five.
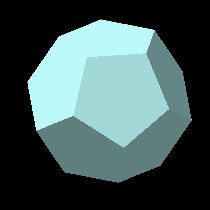
	The dodecahedron has twelve pentagonal faces and is reciprocal to the icosahedron.
	The icosahedron has twenty triangular faces and is reciprocal to the dodecahedron. It has many beautiful stellations.

Star Polyhedra

Johannes Kepler realised that by extending the edges of the dodecahedron until they again met, he could obtain pentagrams or star-pentagons. Since these have equal sides and angles, they meet the definition of regular polygons. Once intersecting edges are allowed, there is no reason not to accept polyhedra with intersecting faces too. Realising this, Kepler was led to the discovery of the two stellated dodecahedra.

Louis Poinsot later realised that if faces are allowed to intersect there are two more regular polyhedra: the great icosahedron and great dodecahedron.

	The small stellated dodecahedron has twelve star-pentagons; five meeting at each vertex.
	The great stellated dodecahedron also has twelve star-pentagons; three meeting at each vertex.
	The great dodecahedron has twelve pentagonal faces just as the ordinary dodecahedron. However they meet at each vertex in a star-pentagonal arrangement.
	The great icosahedron has twenty triangular faces just as the ordinary icosahedron. However they meet at each vertex in a star-pentagonal arrangement.

Regular Compounds

The tetrahedron, cube and octahedron can occur in various regular compounds: arrangements of multiple solid components having more symmetry than the basic component used. A two-dimensional analogue is the six-pointed star which is composed of two equilateral triangles.

	The Stella Octangula, or compound of two tetrahedra was named by Johannes Kepler. In this arrangement the two tetrahedra are reciprocal; the faces of one correspond to the vertices of the other and their edges cross at right angles. Many symmetries are apparent: the two tetrahedra have their vertices at the corners of a cube and their edges form the diagonals of the cube faces. Less obviously, the volume common to both of them is an octahedron. In fact, the two tetrahedra together can be thought of as a variety of octahedron; they have 8 triangular faces arranged symmetrically.
	The compound of ten tetrahedra similarly arises from an icosahedron, which is the interior volume common to all of them: the ten tetrahedra between them have 20 triangular faces. They can also be seen as an arrangement of 5 Stella Octangulae, which suggests the compounds of five cubes and five octahedra below.
	The compound of five tetrahedra is a subset of the compound of ten, found by taking one tetrahedron from each Stella Octangula. It has less symmetry than the interior icosahedron; it has the rotational symmetries but not reflection symmetry. It therefore exists in two mirror-image forms, which is obvious from the twisted appearance.
	The compound of five cubes is suggested by taking the exterior cubes of the five Stella Octangulae of the ten tetrahedra, or the reciprocals of the five octahedra. It is bounded by a dodecahedron, but the interior volume common to all five cubes is not a regular polyhedron.
	The compound of five octahedra is another variety of icosahedron, having 20 triangular faces; the interior common volume is an icosahedron. It is also reciprocal to the compound of five cubes.

Reciprocal Compounds

Some pairs of regular polyhedra are reciprocal: related by swapping faces and vertices. This can be seen in several ways. The face centres of one become the vertices of the other and vice versa. The vertex figures (small polygons found by slicing off a tip near a vertex) become faces of the other and vice versa. The two polyhedra can be placed intersecting so that all their edges cross at right angles.

These compounds are not strictly regular because they have faces of different polygons, but each polyhedron component is regular and they are included here because they illustrate the symmetries involved. For the tetrahedron, the Stella Octangula fills this role because the tetrahedron is reciprocal to itself.

	The cube and the octahedron are reciprocal.
	The dodecahedron and the icosahedron are reciprocal.
	The great stellated dodecahedron and the great icosahedron are reciprocal, although the crossing of the edges occurs inside the stellated dodecahedron and cannot be seen.
	The small stellated dodecahedron and the great dodecahedron are reciprocal. However, the great dodecahedron is entirely inside the small stellated dodecahedron when they are placed together.

Stellations of the Icosahedron

Uniform Polyhedra

Elliptica presents Polyhedra: Computer Graphics from the 90s

Home